Ход работы:

1. Изучить (повторить) теоретический материал:

• Тема 6. Дифференцирование и интегрирование функций.

2. Получить (уточнить) у преподавателя номер своего варианта и выбрать его из списка:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

3. Если возникли вопросы по условию задач, задайте их преподавателю.

4. Внимательно изучить примеры: Открыть.

5. Выполнить задание для своего варианта.

7. Документ MathCad оформить как отчет по лабораторной работе, включающий в себя:

· номер, название, цель работы;

· номер варианта, текстовые условия задач;

· решение задач с краткими пояснениями.

· номер группы, фамилия и инициалы, дата завершения работы.

8. Сдать преподавателю выполненную работу:

•  Работая в локальной сети колледжа, скопировать папку с работой («№группы_Фамилия_№ЛР») в папку на сетевом сервере: \\Server_uch\_БУФЕР\_Aud_27 (на рабочем столе создан ярлык к папке "_ЛР-сдача").

• Работая не в колледже, создать файл-архив папки с работой, зайти на сайте "Образовательный портал" в раздел "Обратная связь", заполнить поля формы, прикрепить свой файл-архив и отправить его преподавателю.

9. Оценки по проверенным работам можно посмотреть в электронном журнале:

• Работая в локальной сети колледжа, откройте ярлык на рабочем столе "Журнал".

• Работая не в колледже, зайти на сайте "Образовательный портал" в раздел "Учебные журналы", открыть журнал текущего семестра.

Индивидуальные задания

Вариант 1.

1. Найти первую и вторую производные функции f(x). Построить графики функции f(x) и ее производных. Найти значение функции и ее производных в точке x = 1:

2 балла.

2. Найти первообразную (неопределенный интеграл) функции f(x). Построить графики функции f(x) и ее первообразной. Вычислить определенный интеграл функции f(x) на отрезке [2;5]:

2 балла.

3. Найти площадь фигуры, ограниченной линиями:

3 балла.

4. Задан закон движения тела как функция координаты (положения) от времени. Значения Xm, w, f подобрать самостоятельно, как исходные данные. Найти уравнения скорости и ускорения движения тела как функции от времени. Определить положение, скорость и ускорение в момент времени t=2 с. Построить графики x(t), v(t), a(t).

 см

3 балла.

Вариант 2.

1. Найти первую и вторую производные функции f(x). Построить графики функции f(x) и ее производных. Найти значение функции и ее производных на отрезке [1; 3] с шагом 0.5:

2 балла.

2. Найти первообразную (неопределенный интеграл) функции f(x). Построить графики функции f(x) и ее первообразной. Вычислить определенный интеграл функции f(x) на отрезке [1;3]:

2 балла.

3. Найти длину дуги кривой заданной уравнением y = f(x), заключенной между вертикальными прямыми x = 1 и x = 3.

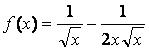
3 балла.

4. Задан закон изменения ускорения движения тела как функция от времени. Найти уравнения скорости движения и положения тела как функции от времени. Начальные условия: v(0)=2 м/c; s(0)=0 м. Определить положение, скорость и ускорение на отрезке времени t=[0;5] c шагом 1 с. Построить графики s(t), v(t), a(t). Решить задачу для k>0 и k<0, сравнить результаты.

a(t) = k*t (м/с2).

3 балла.

Вариант 3.

1. Найти первую и вторую производные функции f(x). Построить графики функции f(x) и ее производных. Найти значение функции и ее производных в точке x = 2:

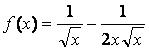
2 балла.

2. Найти первообразную (неопределенный интеграл) функции f(x). Построить графики функции f(x) и ее первообразной. Вычислить определенный интеграл функции f(x) на отрезке [0;π]:

2 балла.

3. Найти площадь фигуры, ограниченной линиями:

3 балла.

4. Найти уравнение зависимости работы электрического тока на участке цепи от времени W(t), если известен закон изменения тока во времени i(t) и сопротивление участка цепи R. Найти значение тока и работы в момент времени t=1 c. Построить графики i(t), W(t). Задачу решить для k<0 и k>0.

i(t) = e^k*t (А).

3 балла.

Вариант 4.

1. Найти первую и вторую производные функции f(x). Построить графики функции f(x) и ее производных. Найти значение функции и ее производных на отрезке [0;π] с шагом π/4:

2 балла.

2. Найти первообразную (неопределенный интеграл) функции f(x). Построить графики функции f(x) и ее первообразной. Вычислить определенный интеграл функции f(x) на отрезке [1;2]:

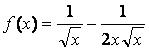
2 балла.

3. Найти длину дуги кривой заданной уравнением y = f(x), заключенной между вертикальными прямыми x = -0.5 и x = 0.5.

3 балла.

4. Найти уравнение зависимости энергии заряженного конденсатора от времени W(t), если известна функциональная зависимость напряжения между пластинами конденсатора от времени u(t) и постоянный ток I=2.5 А. Определить значение W(t) при t=7 с. Построить графики u(t), W(t).

 (В).

3 балла.

Вариант 5.

1. Найти первую и вторую производные функции f(x). Построить графики функции f(x) и ее производных. Найти значение функции и ее производных в точке x = -1:

2 балла.

2. Найти первообразную (неопределенный интеграл) функции f(x). Построить графики функции f(x) и ее первообразной. Вычислить определенный интеграл функции f(x) на отрезке [2;4]:

2 балла.

3. Найти площадь фигуры, ограниченной линиями:

3 балла.

4. Найти уравнение зависимости индуцированного в катушке напряжения от времени u(t), если известна функциональная зависимость магнитного потока от времени Ф(t) и число витков в катушке N=250. Определить значение u(t) при t=2 с. Построить графики Ф(t), u(t).

 ^(В∙с)

3 балла.

Вариант 6.

1. Найти первую и вторую производные функции f(x). Построить графики функции f(x) и ее производных. Найти значение функции и ее производных на отрезке [2;10] с шагом 1:

2 балла.

2. Найти первообразную (неопределенный интеграл) функции f(x). Построить графики функции f(x) и ее первообразной. Вычислить определенный интеграл функции f(x) на отрезке [-1;1]:

2 балла.

3. Найти длину дуги кривой заданной уравнением y = f(x), заключенной между вертикальными прямыми x = 1 и x = 5.

3 балла.

4. Найти уравнение зависимости индуцированного в проводнике напряжения от времени u(t) (явление самоиндукции), если известна функциональная зависимость тока от времени I(t) и индуктивность проводника L=150 Гн. Определить значение u(t) при t=2.5 с. Построить графики I(t), u(t).

 (А).

3 балла.

Вариант 7.

1. Найти первую и вторую производные функции f(x). Построить графики функции f(x) и ее производных. Найти значение функции и ее производных в точке x = 5:

f(x) = x² + 2sin(x)

2 балла.

2. Найти первообразную (неопределенный интеграл) функции f(x). Построить графики функции f(x) и ее первообразной. Вычислить определенный интеграл функции f(x) на отрезке [1;3]:

2 балла.

3. Найти площадь фигуры, ограниченной линиями на отрезке [0; 2]:

3 балла.

4. Задан закон движения тела как функция координаты (положения) от времени. Значения So, Vo, a подобрать самостоятельно, как исходные данные. Найти уравнения скорости и ускорения движения тела как функции от времени. Определить положение, скорость и ускорение в момент времени t=1.2 с. Построить графики s(t), v(t), a(t).

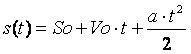 м

3 балла.

Вариант 8.

1. Найти первую и вторую производные функции f(x). Построить графики функции f(x) и ее производных. Найти значение функции и ее производных на отрезке [1; 2] с шагом 0.2:

2 балла.

2. Найти первообразную (неопределенный интеграл) функции f(x). Построить графики функции f(x) и ее первообразной. Вычислить определенный интеграл функции f(x) на отрезке [2;5]:

f(x) = 2x² - x + 1

2 балла.

3. Найти длину дуги кривой заданной уравнением y = f(x), заключенной между вертикальными прямыми x = 1 и x = 3.

3 балла.

4. Задан закон изменения ускорения движения тела как функция от времени. Найти уравнения скорости движения и положения тела как функции от времени. Начальные условия: v(0)=2 м/c; s(0)=0 м. Определить положение, скорость и ускорение на отрезке времени t=[0;5] c шагом 1 с. Построить графики s(t), v(t), a(t). Решить задачу для нескольких значений k.

м/с²

3 балла.

Вариант 9.

1. Найти первую и вторую производные функции f(x). Построить графики функции f(x) и ее производных. Найти значение функции и ее производных в точке x = 1.2:

2 балла.

2. Найти первообразную (неопределенный интеграл) функции f(x). Построить графики функции f(x) и ее первообразной. Вычислить определенный интеграл функции f(x) на отрезке [5;10]:

2 балла.

3. Найти площадь фигуры, ограниченной линиями:

3 балла.

4. Найти уравнение зависимости мгновенного значения напряжения в генераторе переменного тока от времени u(t), если известна функциональная зависимость магнитного потока от времени Ф(t) и число витков в катушке генератора N=100. Определить значение u(t) при t=4 с. Построить графики Ф(t), u(t).

 (В∙с).

где B – магнитная индукция [Тл]; A – площадь витка в катушке генератора [м²]; w – угловая частота [c^-1]. Значение этих величин задать самостоятельно, как исходные данные.

3 балла.

Вариант 10.

1. Найти первую и вторую производные функции f(x). Построить графики функции f(x) и ее производных. Найти значение функции и ее производных на отрезке [2; 3] с шагом 0.1:

2 балла.

2. Найти первообразную (неопределенный интеграл) функции f(x). Построить графики функции f(x) и ее первообразной. Вычислить определенный интеграл функции f(x) на отрезке [-π/4;π/4]:

2 балла.

3. Найти длину дуги кривой заданной уравнением y = f(x), заключенной между вертикальными прямыми x = -0.5 и x = 0.4.

f(x) = 2cos(3x+2)

3 балла.

4. Найти уравнение зависимости мгновенного значения тока в проводнике от времени i(t), если известна функциональная зависимость заряда, протекающего через поперечное сечение проводника от времени q(t). Определить значение i(t) при t=3 с. Построить графики q(t), i(t).

 (К).

3 балла.

Вариант 11.

1. Найти первую и вторую производные функции f(x). Построить графики функции f(x) и ее производных. Найти значение функции и ее производных в точке x = 3:

2 балла.

2. Найти первообразную (неопределенный интеграл) функции f(x). Построить графики функции f(x) и ее первообразной. Вычислить определенный интеграл функции f(x) на отрезке [1;4]:

f(x) = (1 + x)³

2 балла.

3. Найти площадь фигуры, ограниченной линиями:

3 балла.

4. Найти уравнение зависимости заряда, протекающего через поперечное сечение проводника от времени q(t), если известна функциональная зависимость мгновенного значения тока в проводнике от времени i(t). Начальное условие: q(0) = 0. Определить значение q(t) при t=2 с. Построить графики q(t), i(t). Значение Im и w задать самостоятельно, как исходные данные.

 (А)

3 балла.

Вариант 12.

1. Найти первую и вторую производные функции f(x). Построить графики функции f(x) и ее производных. Найти значение функции и ее производных на отрезке [0; 5] с шагом 0.5:

f(x) = 2cos(3x+2) + e^2x

2 балла.

2. Найти первообразную (неопределенный интеграл) функции f(x). Построить графики функции f(x) и ее первообразной. Вычислить определенный интеграл функции f(x) на отрезке [0.1;0.3]:

2 балла.

3. Найти длину дуги кривой заданной уравнением y = f(x), заключенной между вертикальными прямыми x = 1 и x = 2.

3 балла.

4. Найти уравнение зависимости работы электрического тока A(t), если известны функциональные зависимости мгновенных значений тока и напряжения от времени i(t), u(t). Определить значение A(t) при t=10 с. Построить графики A(t), i(t), u(t). Значения Im, Um, w и f задать самостоятельно, как исходные данные.

3 балла.

Вариант 13.

1. Найти первую и вторую производные функции f(x). Построить графики функции f(x) и ее производных. Найти значение функции и ее производных в точке x = 0:

2 балла.

2. Найти первообразную (неопределенный интеграл) функции f(x). Построить графики функции f(x) и ее первообразной. Вычислить определенный интеграл функции f(x) на отрезке [0;5]:

2 балла.

3. Найти точки экстремума функции f(x) на отрезке [-5;0], решив уравнение f '(x) = 0. Построить графики функции f(x) и ее производной.

3 балла.

4. Найти работу по перемещению тела вдоль оси X под действием силы F(x) из точки x₁=0 в точку x₂=5 м, направленной вдоль оси X.

 ^(н).

3 балла.

Вариант 14.

1. Найти первую и вторую производные функции f(x). Построить графики функции f(x) и ее производных. Найти значение функции и ее производных в точке x = 1:

2 балла.

2. Найти первообразную (неопределенный интеграл) функции f(x). Построить графики функции f(x) и ее первообразной. Вычислить определенный интеграл функции f(x) на отрезке [-0.5;0.5]:

f(x) = cos(3x²)

2 балла.

3. Вычислить длину кривой, заданной параметрическими уравнениями:

3 балла.

4. Найти заряд, протекающий через поперечное сечение проводника, если сила тока в проводнике является функцией времени i(t) от момента времени t₁=0 до t₂=3 с. Значения Im и w задать самостоятельно.

^(А).

3 балла.

Вариант 15.

1. Найти первую и вторую производные функции f(x). Построить графики функции f(x) и ее производных. Найти значение функции и ее производных в точке x = 1.3:

2 балла.

2. Найти первообразную (неопределенный интеграл) функции f(x). Построить графики функции f(x) и ее первообразной. Вычислить определенный интеграл функции f(x) на отрезке [0;0.5]:

f(x) = 2cos(2x)

2 балла.

3. Найти точки экстремума функции f(x) на отрезке [-2;2], решив уравнение f '(x) = 0. Построить графики функции f(x) и ее производной.

3 балла.

4. Найти работу по перемещению тела вдоль оси X под действием силы F(x,t) из точки x₁=0 в точку x₂=5 м, направленной вдоль оси X за интервал времени от t₁=2 с до t₂=8 с.

 ^(н).

3 балла.

Вариант 16.

1. Найти первую и вторую производные функции f(x). Построить графики функции f(x) и ее производных. Найти значение функции и ее производных в точке x = 2:

2 балла.

2. Найти первообразную (неопределенный интеграл) функции f(x). Построить графики функции f(x) и ее первообразной. Вычислить определенный интеграл функции f(x) на отрезке [1;2]:

f(x) = x² + 2x - 1

2 балла.

3. Вычислить длину кривой, заданной параметрическими уравнениями:

3 балла.

4. Найти заряд, протекающий через поперечное сечение проводника, если сила тока в проводнике является функцией времени i(t) от момента времени t1=0 до t2=3 с. Значения Im, w, f задать самостоятельно.

^(А).

3 балла.

Вариант 17.

1. Найти первую и вторую производные функции f(x). Построить графики функции f(x) и ее производных. Найти значение функции и ее производных в точке x = 2.5:

2 балла.

2. Найти первообразную (неопределенный интеграл) функции f(x). Построить графики функции f(x) и ее первообразной. Вычислить определенный интеграл функции f(x) на отрезке [0;π/2]:

f(x) = 2x² - 3x + 1

2 балла.

3. Найти точки экстремума функции f(x) на отрезке [-1;4], решив уравнение f '(x) = 0. Построить графики функции f(x) и ее производной.

3 балла.

4. Найти работу, совершенную газом при расширении от объема V₁=1 м³ до V₂=4 м³, если давление газа является функцией его объема:

 ^(Па).

3 балла.

Вариант 18.

1. Найти первую и вторую производные функции f(x). Построить графики функции f(x) и ее производных. Найти значение функции и ее производных в точке x = 3:

2 балла.

2. Найти первообразную (неопределенный интеграл) функции f(x). Построить графики функции f(x) и ее первообразной. Вычислить определенный интеграл функции f(x) на отрезке [0;2]:

f(x) = x² + 2x - x

2 балла.

3. Вычислить длину кривой, заданной параметрическими уравнениями:

3 балла.

4. Найти работу, совершенную над газом для его сжатия от объема V₁=10 м³ до V₂=4 м³, если давление газа является функцией его объема:

 ^(кПа).

3 балла.

Вариант 19.

1. Найти первую и вторую производные функции f(x). Построить графики функции f(x) и ее производных. Найти значение функции и ее производных в точке x = 0:

2 балла.

2. Найти первообразную (неопределенный интеграл) функции f(x). Построить графики функции f(x) и ее первообразной. Вычислить определенный интеграл функции f(x) на отрезке [-5;5]:

2 балла.

3. Найти точки экстремума функции f(x) на отрезке [0;2], решив уравнение f '(x) = 0. Построить графики функции f(x) и ее производной.

3 балла.

4. Задан закон движения тела как функция координаты (положения) от времени. Значения Xm, w, f подобрать самостоятельно, как исходные данные. Найти уравнения скорости и ускорения движения тела как функции от времени. Определить положение, скорость и ускорение в момент времени t=1 с. Построить графики x(t), v(t), a(t).

 см

3 балла.

Вариант 20.

1. Найти первую и вторую производные функции f(x). Построить графики функции f(x) и ее производных. Найти значение функции и ее производных в точке x = -1:

2 балла.

2. Найти первообразную (неопределенный интеграл) функции f(x). Построить графики функции f(x) и ее первообразной. Вычислить определенный интеграл функции f(x) на отрезке [-1;0]:

f(x) = sin(2x - 1) + cos(2x + 1)

2 балла.

3. Вычислить длину кривой, заданной параметрическими уравнениями:

3 балла.

4. Задан закон изменения ускорения движения тела как функция от времени. Найти уравнения скорости движения и положения тела как функции от времени. Начальные условия: v(0)=0 м/c; s(0)=1 м. Определить положение, скорость и ускорение на отрезке времени t=[0;10] c шагом 1 с. Построить графики s(t), v(t), a(t).

a(t) = 2t² - 3t + 1 (м/с2).

3 балла.

Вариант 21.

1. Найти первую и вторую производные функции f(x). Построить графики функции f(x) и ее производных. Найти значение функции и ее производных в точке x = 0.3:

2 балла.

2. Найти первообразную (неопределенный интеграл) функции f(x). Построить графики функции f(x) и ее первообразной. Вычислить определенный интеграл функции f(x) на отрезке [0;3]:

f(x) = 3x³ + 2x² - 1.5x + 2

2 балла.

3. Найти точки экстремума функции f(x) на отрезке [-1;1], решив уравнение f '(x) = 0. Построить графики функции f(x) и ее производной.

3 балла.

4. Задан закон изменения ускорения движения тела как функция от времени. Найти уравнения скорости движения и положения тела как функции от времени. Начальные условия: v(0)=2.5 м/c; s(0)=-1 м. Определить положение, скорость и ускорение на отрезке времени t=[0;5] c шагом 0.5 с. Построить графики s(t), v(t), a(t).

a(t) = -3t² + 2t - 1 (м/с2).

3 балла.

Вариант 22.

1. Найти первую и вторую производные функции f(x). Построить графики функции f(x) и ее производных. Найти значение функции и ее производных в точке x = 1:

2 балла.

2. Найти первообразную (неопределенный интеграл) функции f(x). Построить графики функции f(x) и ее первообразной. Вычислить определенный интеграл функции f(x) на отрезке [0;0.5]:

f(x) = (sin(x) + cos(x))²

2 балла.

3. Вычислить длину кривой, заданной параметрическими уравнениями:

3 балла.

4. Найти уравнение зависимости работы электрического тока на участке цепи от времени W(t), если известен закон изменения тока во времени i(t) и сопротивление участка цепи R. Найти значение тока и работы в момент времени t=5 c. Построить графики i(t), W(t).

i(t) = 2.5e^-3*t (А).

3 балла.

Вариант 23.

1. Найти первую и вторую производные функции f(x). Построить графики функции f(x) и ее производных. Найти значение функции и ее производных в точке x = 1.7:

2 балла.

2. Найти первообразную (неопределенный интеграл) функции f(x). Построить графики функции f(x) и ее первообразной. Вычислить определенный интеграл функции f(x) на отрезке [0;π]:

f(x) = exp(2x - x)

2 балла.

3. Найти точки экстремума функции f(x) на отрезке [0;5], решив уравнение f '(x) = 0. Построить графики функции f(x) и ее производной.

3 балла.

4. Найти уравнение зависимости работы электрического тока на участке цепи от времени W(t), если известен закон изменения тока во времени i(t) и сопротивление участка цепи R. Найти значение тока и работы в момент времени t=5 c. Построить графики i(t), W(t).

i(t) = 2cos(1.2t - π) (А).

3 балла.

Вариант 24.

1. Найти первую и вторую производные функции f(x). Построить графики функции f(x) и ее производных. Найти значение функции и ее производных в точке x = 0.25:

2 балла.

2. Найти первообразную (неопределенный интеграл) функции f(x). Построить графики функции f(x) и ее первообразной. Вычислить определенный интеграл функции f(x) на отрезке [2;3]:

f(x) = sin(2x + 1)+cos(3x-1)

2 балла.

3. Вычислить длину кривой, заданной параметрическими уравнениями:

3 балла.

4. Найти уравнение зависимости энергии заряженного конденсатора от времени W(t), если известна функциональная зависимость напряжения между пластинами конденсатора от времени u(t) и постоянный ток I=0.5 А. Определить значение W(t) при t=5 с. Построить графики u(t), W(t).

u(t) = 12cos(60t + π/2) (В)

3 балла.

Вариант 25.

1. Найти первую и вторую производные функции f(x). Построить графики функции f(x) и ее производных. Найти значение функции и ее производных в точке x = 0.5:

f(x) = cos(x) * sin(x)

2 балла.

2. Найти первообразную (неопределенный интеграл) функции f(x). Построить графики функции f(x) и ее первообразной. Вычислить определенный интеграл функции f(x) на отрезке [0;10]:

f(x) = 4x³ - 3x + ln(x²)

2 балла.

3. Найти точки экстремума функции f(x) на отрезке [-2;2], решив уравнение f '(x) = 0. Построить графики функции f(x) и ее производной.

f(x) = -2cos²(x)

3 балла.

4. Найти уравнение зависимости индуцированного в катушке напряжения от времени u(t), если известна функциональная зависимость магнитного потока от времени Ф(t) и число витков в катушке N=500. Определить значение u(t) при t=5 с. Построить графики Ф(t), u(t).

Ф(t) = 1.2sin²(2t) (В*с)

3 балла.

Вариант 26.

1. Найти первую и вторую производные функции f(x). Построить графики функции f(x) и ее производных. Найти значение функции и ее производных в точке x = 2.3:

f(x) = 4x³ - 3x + ln(x²)

2 балла.

2. Найти первообразную (неопределенный интеграл) функции f(x). Построить графики функции f(x) и ее первообразной. Вычислить определенный интеграл функции f(x) на отрезке [-2π; 2π]:

f(x) = cos(x) * sin(x)

2 балла.

3. Вычислить длину кривой, заданной параметрическими уравнениями:

x(t) = cos³(t);  y(t) = sin²(t)

3 балла.

4. Задан закон движения тела как функция координаты (положения) от времени. Найти уравнения скорости и ускорения движения тела как функции от времени. Определить положение, скорость и ускорение в момент времени t=2 с. Построить графики s(t), v(t), a(t).

s(t) = 1.5t + 4.5t² (м)

3 балла.

 

---