ОКР MathCad.

Задания к обязательной контрольной работе № 1 по учебной дисциплине

«Информационные технологии».

для гр. "в, ппа, ппу"

Выполняется по материалам раздела «Применение автоматизированной системы математических вычислений MathCad для решения прикладных задач».

Работа выполняется в электронном формате. Файлы работы сдать (скопировать по сети) не позднее, чем за 5 минут до окончания занятия.

Скопировать папку с работой («№группы_Фамилия_ОКР1») в папку на сетевом сервере: \\Aud27_0\ЛР-сдача (на рабочем столе создан ярлык к папке).

Уточните у преподавателя номер своего варианта и выберите его из списка:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

Вариант 1.

Задача 1 (3 балла):

Определить следующую функцию y(x) = x² - 2sin(x) и вывести ее таблицу значений на отрезке от -5 до 5 с шагом 0.5. Построить график функции.

Задача 2 (3 балла):

Определить следующую функцию y(a,b) с условиями сравнения и вывести таблицу ее значений для a от 0 до 5 с шагом 0.5 при b=2:

Задача 3 (4 баллов):

Решить следующую физическую задачу, используя соответствующие размерные переменные:

Дан железный проводник длиной 2 м и площадью поперечного сечения S мм². Определить сопротивление проводника при температуре t^○ С. Построить график зависимости сопротивления от площади поперечного сечения R(S). Анимировать график для различных значений температуры t.

Вариант 2.

Задача 1 (3 балла):

Построить в одной системе координат графики следующих функций: f1(x) = cos(2x); f2(x) = cos(3x); f3(x) = f1(x) + f2(x)

Задача 2 (3 балла):

Задан закон движения тела как функция координаты (положения в метрах) от времени (в секундах). Значения So, Vo, a подобрать самостоятельно, как исходные данные. Найти уравнения скорости и ускорения движения тела как функции от времени. Определить положение, скорость и ускорение в момент времени t=1.2 с. Построить графики s(t), v(t), a(t).

Задача 3 (4 баллов):

Решить следующую физическую задачу, используя соответствующие размерные переменные:

Какая сила тока создается в стартере автомобиля, если он включается на t с и в нем проходит заряд Q Кл? Построить график зависимости силы тока от заряда I(Q). Анимировать график для различных значений времени t.

Вариант 3.

Задача 1 (3 балла):

Определить следующую функцию:

вывести таблицу значений функции на отрезке от 0 до 10 с шагом 1. Построить ее график.

Задача 2 (3 балла):

Определить следующую функцию y(a,b):

Вывести таблицу ее значений для a от -1 до 1 с шагом 0.1 при b = -1.

Задача 3 (4 баллов):

Решить следующую физическую задачу, используя соответствующие размерные переменные:

Конденсатор емкостью C мкФ заряжается до напряжения U В за t с. Каково среднее значение силы зарядного тока? Построить график зависимости среднего значения зарядного тока от емкости конденсатора I(C). Анимировать график для различных значений напряжения U.

Вариант 4.

Задача 1 (3 балла):

Вычислить:

для следующих наборов исходных данных: a) x = 2; n = 2; b) x = -2; n = 3; c) x = -28; n = 5.

Задача 2 (3 балла):

Найти площадь фигуры, ограниченной линиями:

Задача 3 (4 баллов):

Для электрической цепи постоянного тока, заданной на рисунке, выполнить следующее:

- составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях схемы;

- решить составленную систему двумя способами (матричным и блоком Given) в среде MathCad и сравнить полученные результаты;

- составить и проверить баланс мощностей для схемы.

Числовые параметры схемы:

E₁, В	E₂, В	R₁, Ом	R₂, Ом	R₃, Ом	R₄, Ом	R₅, Ом	R₆, Ом	r₀₁, Ом	r₀₂, Ом
30	40	26	64	43	35	51	16	2	2

Вариант 5.

Задача 1 (3 балла):

Вычислить:

для следующих наборов исходных данных: a) x = 2; n = 2; b) x = -2; n = 3; c) x = -12; n = 30

Задача 2 (3 балла):

Решить следующую физическую задачу, используя соответствующие размерные переменные:

Можно ли включить в сеть с напряжением 220 В реостаты, на которых написано: 1) 30 Ом, 5 А; 2) 2000 Ом, 0.2 А?

Задача 3 (4 баллов):

Для электрической цепи постоянного тока, заданной на рисунке, выполнить следующее:

- составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях схемы;

- составить и проверить баланс мощностей для схемы.

Числовые параметры схемы:

E₁, В	E₂, В	R₁, Ом	R₂, Ом	R₃, Ом	R₄, Ом	R₅, Ом	R₆, Ом	r₀₁, Ом	r₀₂, Ом
30	40	16	63	34	42	25	52	3	2

Вариант 6.

Задача 1 (3 балла):

Построить график функции, учитывая её область определения и точки разрыва:

Задача 2 (3 балла):

Решить следующую физическую задачу, используя соответствующие размерные переменные:

Найти силу тока в стальном проводнике длиной 10 м и сечением 2 мм², на который подано напряжение 12 мВ.

Задача 3 (4 баллов):

К зажимам электрической цепи подключен источник синусоидального напряжения:

частотой f=50 Гц.

Числовые параметры схемы:

Um, В	ψ_U, ^○	R₁, Ом	R₂, Ом	L₁, мГн	L₂, мГн	С₁, мкФ	С₂, мкФ
180	60	25	50	79.5	127.2	318	79.5

Выполнить следующее:

1) Начертить схему замещения электрической цепи (можно использовать программы КОМПАС, Word, Paint или др.) и вставить ее в свой документ MathCad.

2) Рассчитать реактивные сопротивления элементов цепи.

3) Определить действующие значения токов во всех ветвях цепи.

4) Записать уравнение мгновенного значения тока источника.

5) Составить и проверить баланс активных и реактивных мощностей.

Вариант 7.

Задача 1 (3 балла):

Построить график функции, учитывая её область определения и точки разрыва:

Задача 2 (3 балла):

Решить следующую физическую задачу, используя соответствующие размерные переменные:

Цепь состоит из трех последовательно соединенных проводников, подключенных к источнику с напряжением 24 В. Сопротивление первого проводника 4 Ом, второго 6 Ом, и напряжение на концах третьего проводника 4 В. Найти силу тока в цепи, сопротивление третьего проводника и напряжения на концах первого и второго проводников.

Задача 3 (4 баллов):

К зажимам электрической цепи подключен источник синусоидального напряжения:

частотой f=50 Гц.

Числовые параметры схемы:

Um, В	ψ_U, ^○	R₁, Ом	R₂, Ом	L₁, мГн	L₂, мГн	С₁, мкФ	С₂, мкФ
540	-45	50	100	159	254.4	63.5	39.8

Выполнить следующее:

2) Рассчитать реактивные сопротивления элементов цепи.

3) Определить действующие значения токов во всех ветвях цепи.

4) Записать уравнение мгновенного значения тока источника.

5) Составить и проверить баланс активных и реактивных мощностей.

Вариант 8.

Задача 1 (3 балла):

Построить графики функций в одной системе координат: f1(x) = 2sin(x); f2(x) = sin(2x); f3(x) = f1(x) + f2(x)

Задача 2 (3 балла):

Решить следующую физическую задачу, используя соответствующие размерные переменные:

Электрическую лампу сопротивлением 240 Ом, рассчитанную на напряжение 120 В, надо питать от сети с напряжением 220 В. Какой длины нихромовый проводник сечением 0.55 мм² надо включить последовательно с лампой?

Задача 3 (4 баллов):

К зажимам электрической цепи подключен источник синусоидального напряжения:

частотой f=50 Гц.

Числовые параметры схемы:

Um, В	ψ_U, ^○	R₁, Ом	R₂, Ом	L₁, мГн	L₂, мГн	С₁, мкФ	С₂, мкФ
180	0	20	30	127.2	63.8	159	159

Выполнить следующее:

1) Начертить схему замещения электрической цепи (можно использовать программы Компас, Word, Paint или др.) и вставить ее в свой документ MathCad.

2) Рассчитать реактивные сопротивления элементов цепи.

3) Определить действующие значения токов во всех ветвях цепи.

4) Записать уравнение мгновенного значения тока источника.

5) Составить и проверить баланс активных и реактивных мощностей.

Вариант 9.

Задача 1 (3 балла):

Построить график функции, заданной параметрическими уравнениями: x(t) = a*cos(t); y(t) = b*sin(t)

Задача 2 (3 балла):

Функция задана уравнением в полярной системе координат R=f(a). Построить график этой функции в полярной и прямоугольной системах координат.

Задача 3 (4 баллов):

Задан закон изменения ускорения движения тела как функция от времени (м/с²):

a(t) = 2t - 1

Найти уравнения скорости движения и положения тела как функции от времени. Начальные условия: v(0)=2 м/c; s(0)=0 м. Определить положение, скорость и ускорение на отрезке времени t=[0;5] c шагом 1 с. Построить графики s(t), v(t), a(t). Решить задачу для нескольких значений k.

Вариант 10.

Задача 1 (3 балла):

Построить график поверхности:

Задача 2 (3 балла):

Заполнить квадратную матрицу 3-го порядка целыми случайными числами с диапазоном значений от -10 до 10. Вычислить:

- определитель матрицы;

- обратную матрицу;

- транспонированную матрицу;

- максимальный и минимальный элементы матрицы;

- среднее значение элементов матрицы;

- минимум между средними значениями 0-го и 2-го столбца;

- сумму элементов, стоящих на главной диагонали матрицы;

- максимальное значение в нижнем левом прямоугольнике матрицы, размером 2 х 2;

- отсортировать матрицу по элементам 2-й строки.

Задача 3 (4 баллов):

Найти уравнение зависимости заряда, протекающего через поперечное сечение проводника от времени q(t), если известна функциональная зависимость мгновенного значения тока в проводнике от времени i(t) (А):

Начальное условие: q(0) = 0. Определить значение q(t) при t=2 с. Построить графики q(t), i(t). Значение Im и w задать самостоятельно, как исходные данные.

Вариант 11.

Задача 1 (3 балла):

Построить график поверхности: z(x,y) = a*cos(b*x*y)

Задача 2 (3 балла):

Заполнить квадратную матрицу 5-го порядка целыми случайными числами с диапазоном значений от 0 до 100. Вычислить:

- определитель матрицы;

- обратную матрицу;

- транспонированную матрицу;

- разность между максимальным и минимальным элементами матрицы;

- среднее значение элементов матрицы;

- отношение средних значений 2-го и 3-го столбца;

- сумму элементов, стоящих на главной диагонали матрицы;

- минимальное значение в верхнем левом прямоугольнике матрицы, размером 2 х 2;

- отсортировать матрицу по элементам 0-го столбца.

Задача 3 (4 баллов):

Для электрической цепи постоянного тока, заданной на рисунке, выполнить следующее:

- составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях схемы;

- составить и проверить баланс мощностей для схемы.

Числовые параметры схемы:

E₁, В	E₂, В	R₁, Ом	R₂, Ом	R₃, Ом	R₄, Ом	R₅, Ом	R₆, Ом	r₀₁, Ом	r₀₂, Ом
20	30	54	43	32	26	51	15	2	2

Вариант 12.

Задача 1 (3 балла):

Определить 2 вектора V1 и V2 одинаковой размерности (значения элементов задать самостоятельно). Вычислить:

- скалярное произведение векторов;

- векторные произведения векторов;

- разность модулей векторов;

- сумму элементов двух векторов;

- разность между максимальным элементом вектора V2 и минимальным значением вектора V1;

- разность между средними значениями двух векторов;

- упорядочить элементы вектора V1 по возрастанию их значений;

- упорядочить элементы вектора V2 по убыванию их значений;

Задача 2 (3 балла):

Решить систему уравнений:

Задача 3 (4 баллов):

Найти уравнение зависимости работы электрического тока A(t), если известны функциональные зависимости мгновенных значений тока и напряжения от времени i(t), u(t). Определить значение A(t) при t=10 с. Построить графики A(t), i(t), u(t). Значения Im, Um, w и f задать самостоятельно, как исходные данные.

Вариант 13.

Задача 1 (3 балла):

Найти наименьший положительный корень уравнения x² - 2sin(x) = 0 с точностью 10^-4.

Задача 2 (3 балла):

Найти первую и вторую производные функции f(x). Построить графики функции f(x) и ее производных.

Задача 3 (4 баллов):

Найти уравнение зависимости мгновенного значения напряжения в генераторе переменного тока от времени u(t), если известна функциональная зависимость магнитного потока от времени Ф(t) и число витков в катушке генератора N=100. Определить значение u(t) при t=4 с. Построить графики Ф(t), u(t).

где B – магнитная индукция [Тл]; A – площадь витка в катушке генератора [м²]; w – угловая частота [c^-1]. Значение этих величин задать самостоятельно, как исходные данные.

Вариант 14.

Задача 1 (3 балла):

Найти наименьший по модулю корень уравнения x³ - 2sin(3x) = 0 с точностью 10^-6.

Задача 2 (3 балла):

Найти площадь фигуры, ограниченной линиями:

Задача 3 (4 баллов):

Для электрической цепи постоянного тока, заданной на рисунке, выполнить следующее:

- составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях схемы;

- составить и проверить баланс мощностей для схемы.

Числовые параметры схемы:

E₁, В	E₂, В	R₁, Ом	R₂, Ом	R₃, Ом	R₄, Ом	R₅, Ом	R₆, Ом	r₀₁, Ом	r₀₂, Ом
50	30	53	34	24	18	25	42	1	1

Вариант 15.

Задача 1 (3 балла):

Найти значение производной функции f(x) на отрезке [1; 3] с шагом 0.5:

Задача 2 (3 балла):

Найти площадь фигуры, ограниченной линиями:

Задача 3 (4 баллов):

Решить следующую физическую задачу, используя соответствующие размерные переменные: На каком расстоянии друг от друга заряды Q₁ Кл и Q₂ Кл взаимодействуют с силой F н? Построить график зависимости расстояния от силы r(F). Анимировать график для различных значений заряда Q₂.

Вариант 16.

Задача 1 (3 балла):

Найти наименьший по модулю корень уравнения f(x) = 0 с точностью 10^-3.

Задача 2 (3 балла):

Найти заряд, протекающий через поперечное сечение проводника, если сила тока в проводнике является функцией времени i(t) от момента времени t1=0 до t2=3 с. Решить задачу для нескольких значений Im, w, f (задать самостоятельно).

Задача 3 (4 баллов):

К зажимам электрической цепи подключен источник синусоидального напряжения:

частотой f=50 Гц.

Числовые параметры схемы:

Um, В	ψ_U, ^○	R₁, Ом	R₂, Ом	L₁, мГн	L₂, мГн	С₁, мкФ	С₂, мкФ
180	60	25	50	79.5	127.2	318	79.5

Выполнить следующее:

2) Рассчитать реактивные сопротивления элементов цепи.

3) Определить действующие значения токов во всех ветвях цепи.

4) Записать уравнение мгновенного значения тока источника.

5) Составить и проверить баланс активных и реактивных мощностей.

Вариант 17.

Задача 1 (3 балла):

Определить следующую функцию:

вывести таблицу значений функции на отрезке от -10 до 10 с шагом 0.5. Построить ее график.

Задача 2 (3 балла):

Найти уравнение зависимости мгновенного значения тока в проводнике от времени i(t), если известна функциональная зависимость заряда, протекающего через поперечное сечение проводника от времени q(t). Определить значение i(t) при t=3 с. Построить графики q(t), i(t).

Задача 3 (4 баллов):

Решить следующую физическую задачу, используя соответствующие размерные переменные:

Какой заряд пройдет через стартер автомобиля, если он включается на t с и потребляет ток I А? Построить график зависимости заряда от силы тока Q(I). Анимировать график для различных значений времени t.

Вариант 18.

Задача 1 (3 балла):

Определить следующую функцию:

вывести таблицу значений функции на отрезке от -2 до 2 с шагом 0.2. Построить ее график.

Задача 2 (3 балла):

Определить следующую функцию y(a,b):

Вывести таблицу ее значений для a от -5 до 5 с шагом 0.5 при b=1 и построить график.

Задача 3 (4 баллов):

Решить следующую физическую задачу, используя соответствующие размерные переменные:

Как долго проходит ток через стартер автомобиля, если он потребляет ток I А и при этом через него проходит заряд в Q Кл? Построить график зависимости времени от заряда t(Q). Анимировать график для различных значений силы тока I.

Вариант 19.

Задача 1 (3 балла):

Вычислить для следующих наборов исходных данных: a) x = 2; n = 2; b) x = -2; n = 3; c) x = 100; n = 10

Задача 2 (3 балла):

Решить следующую физическую задачу, используя соответствующие размерные переменные:

Три проводника с сопротивлением 10, 20 и 30 Ом соединены параллельно. Напряжение на первом сопротивлении 20В. Определите силу тока на каждом сопротивлении и общее сопротивление данного участка цепи.

Задача 3 (4 баллов):

Для электрической цепи постоянного тока, заданной на рисунке, выполнить следующее:

- составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях схемы;

- составить и проверить баланс мощностей для схемы.

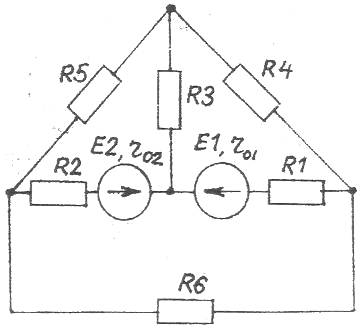
Числовые параметры схемы:

E₁, В	E₂, В	R₁, Ом	R₂, Ом	R₃, Ом	R₄, Ом	R₅, Ом	R₆, Ом	r₀₁, Ом	r₀₂, Ом
30	20	45	53	32	24	61	15	1	1

Вариант 20.

Задача 1 (3 балла):

Вычислить:

для нескольких наборов исходных данных: a) m = 2; n = 2; b) m = 2; n = 3; c) m = 2; n = 4

Задача 2 (3 балла):

Решить следующую физическую задачу, используя соответствующие размерные переменные:

На каком расстоянии друг от друга заряды 1 мкКл и 10 нКл взаимодействуют с силой 9 мН?

Задача 3 (4 баллов):

Для электрической цепи постоянного тока, заданной на рисунке, выполнить следующее:

- составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях схемы;

- составить и проверить баланс мощностей для схемы.

Числовые параметры схемы:

E₁, В	E₂, В	R₁, Ом	R₂, Ом	R₃, Ом	R₄, Ом	R₅, Ом	R₆, Ом	r₀₁, Ом	r₀₂, Ом
20	30	64	43	31	25	52	14	1	2

Вариант 21.

Задача 1 (3 балла):

Вычислить:

для следующих наборов исходных данных: a) x = 2; n = 2; b) x = -2; n = 3; c) x = -20; n = 5

Задача 2 (3 балла):

Решить следующую физическую задачу, используя соответствующие размерные переменные:

В некоторой точке электрического поля на заряд 2 нКл действует сила 0,4 мкН. Найти напряженность поля в этой точке.

Задача 3 (4 баллов):

Для электрической цепи постоянного тока, заданной на рисунке, выполнить следующее:

- составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях схемы;

- составить и проверить баланс мощностей для схемы.

Числовые параметры схемы:

E₁, В	E₂, В	R₁, Ом	R₂, Ом	R₃, Ом	R₄, Ом	R₅, Ом	R₆, Ом	r₀₁, Ом	r₀₂, Ом
30	20	54	42	23	31	16	51	1	2

Вариант 22.

Задача 1 (3 балла):

Построить график функции, учитывая её область определения и точки разрыва:

Задача 2 (3 балла):

Решить следующую физическую задачу, используя соответствующие размерные переменные:

Какую работу совершает электрическое поле при перемещении заряда 20 нКл из точки с потенциалом 700 В в точку с потенциалом 200 В?

Задача 3 (4 баллов):

К зажимам электрической цепи подключен источник синусоидального напряжения:

частотой f=50 Гц.

Числовые параметры схемы:

Um, В	ψ_U, ^○	R₁, Ом	R₂, Ом	L₁, мГн	L₂, мГн	С₁, мкФ	С₂, мкФ
311	30	20	30	63.6	127.2	79.5	53

Выполнить следующее:

2) Рассчитать реактивные сопротивления элементов цепи.

3) Определить действующие значения токов во всех ветвях цепи.

4) Записать уравнение мгновенного значения тока источника.

5) Составить и проверить баланс активных и реактивных мощностей.

Вариант 23.

Задача 1 (3 балла):

Построить график функции и ее таблицу значений на отрезке [0; 2] с шагом 0.1:

Задача 2 (3 балла):

Задача 3 (4 баллов):

К зажимам электрической цепи подключен источник синусоидального напряжения:

частотой f=50 Гц.

Числовые параметры схемы:

Um, В	ψ_U, ^○	R₁, Ом	R₂, Ом	L₁, мГн	L₂, мГн	С₁, мкФ	С₂, мкФ
320	90	40	60	127.2	190.8	39.8	53

Выполнить следующее:

2) Рассчитать реактивные сопротивления элементов цепи.

3) Определить действующие значения токов во всех ветвях цепи.

4) Записать уравнение мгновенного значения тока источника.

5) Составить и проверить баланс активных и реактивных мощностей.

Вариант 24.

Задача 1 (3 балла):

Построить график функции, заданной параметрическими уравнениями:

Задача 2 (3 балла):

Задача 3 (4 баллов):

Найти работу по перемещению тела вдоль оси X под действием силы F(x,t) из точки x1=0 в точку x2=5 м, направленной вдоль оси X за интервал времени от t1=2 с до t2=8 с.